Master the Sudoku Pointing Pairs Technique

What is a Pointing Pair?

A pointing pair occurs when a specific Note (candidate) appears only two or three times within a single 3x3 block, and all those instances happen to be aligned in the same row or column.

Because that number must be the solution for one of those cells inside that block, it effectively "points" along the line. This logical locking means you can safely eliminate that candidate from any other cells in the rest of the row or column outside of that specific block.

How to Find and Apply This Strategy

Identifying this pattern requires a keen eye for candidate distribution. To understand this technique better, let's analyze the example in the bottom-right 3x3 block and its relationship with Column 9.

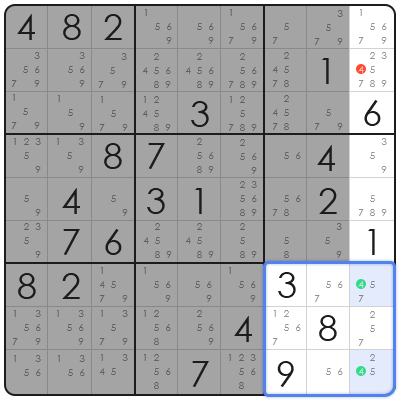
Pointing pairs example - candidate 4 confined to column 9 within bottom-right block ready for elimination

In this specific grid area, we have the following candidates:

Column 9 Notes (Outside Block):

R1C9 = {1, 5, 6, 7, 9}

R2C9 = {2, 3, 4, 5, 7, 8, 9} (The target "victim" cell)

R4C9 = {3, 5, 9}

R5C9 = {5, 7, 8, 9}

Bottom-Right Block Notes:

R7C9 = {4, 5, 7}

R9C9 = {2, 4, 5}

(Other cells in this block do not contain candidate '4')

Step 1: Scan the Notes Inside the Block

Look at the candidates only inside the bottom-right block. We are searching for a number confined to a single line. We find that the candidate '4' only appears in two cells within this box: R7C9 and R9C9.

Step 2: Identify the Locked Candidates

Since both of these cells are located in Column 9, they form this specific pattern. The logic is simple: Number '4' must exist somewhere in the bottom-right block. Since these are the only two possible spots, one of them must be 4. Therefore, the '4' for this block is "locked" into Column 9.

Step 3: Eliminate Notes from the Rest of the Row or Column

Knowing that the '4' for Box 9 is restricted to Column 9, we can clear all other '4's from the rest of the column. This is a powerful candidate eliminator that helps simplify the board.

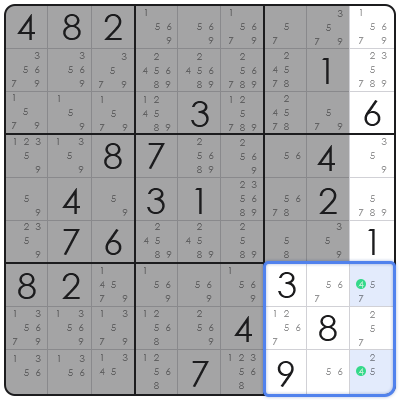
Box-line reduction complete - pointing pairs eliminates candidate 4 from victim cells outside block

In our "victim" cell, R2C9, the notes are {2, 3, 4, 5, 7, 8, 9}. Because our logic dictates that 4 must be in the bottom block, we can safely delete '4' from R2C9 and any other cells in the rest of the row if the pair were aligned horizontally.

Why Mastering This Technique is Essential

While pointing pairs may seem simple, they are the foundation for more advanced strategies like "Pointing Triples" or "Box-Line Reduction." Using this sudoku technique regularly will help you solve Hard Sudoku puzzles where naked singles are no longer visible.

Ready to practice? We encourage you to start a new game of Medium Sudoku or Hard Sudoku to put this theory into action. Can you find a candidate to eliminate from the rest of the row in your next puzzle?

Next Steps

Once you are comfortable with this method, you can proceed to the next strategy: Pointing Triples, which applies the same logic to three cells instead of two.