数独“Y-Wing”法 (Y-Wing) 解题技巧

什么是“Y-Wing”法？

“Y-Wing”法（有时也称为 XY-Wing）是一种数独的进阶解题策略。它与“X-Wing”类似，但它是基于三个角（即三个单元格）而不是四个。这三个单元格中的每一个都必须恰好包含两个候选数（双值格）。

如何发现 Y-Wing

通过查看示例，我们将更容易理解这种技巧。Y-Wing 由三个包含“双值候选数”的单元格组成。我们将它们标记为 AB、AC 和 BC。

第一步：寻找“枢纽”格 (AB)

首先，我们需要找到一个恰好只有两个候选数的单元格。我们将这个单元格称为枢纽 (Pivot)。

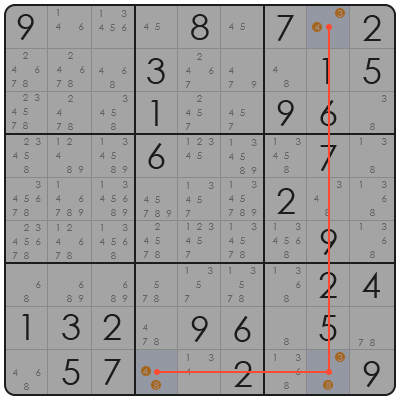
• 枢纽 (AB)： 让我们看 R9C8（第9行第8列）。它的候选数是 {3, 8}。

第二步：寻找两个“钳子”格 (AC 和 BC)

接下来，我们要寻找另外两个同样只有 2 个候选数的单元格（称为钳子或双翼）。这些单元格必须能“看到”枢纽（即在同一行、同一列或同一宫内），并且与枢纽共享一个数字。

• 钳子 1 (AC)： 让我们看 R1C8。它的候选数是 {3, 4}。它（通过第 8 列）连接到枢纽 R9C8，并共享数字 '3'。
• 钳子 2 (BC)： 让我们看 R9C4。它的候选数是 {4, 8}。它（通过第 9 行）连接到枢纽 R9C8，并共享数字 '8'。

这两个钳子共同拥有、但枢纽却没有的那个数字，就是**“受害”数字**（目标删除数）。在这个例子中，它是 4。

第三步：寻找受害格并排除

现在，让我们寻找任何同时能“看到”（相交）两个钳子的单元格。

• 钳子 1 (R1C8) 位于第 1 行第 8 列。
• 钳子 2 (R9C4) 位于第 9 行第 4 列。

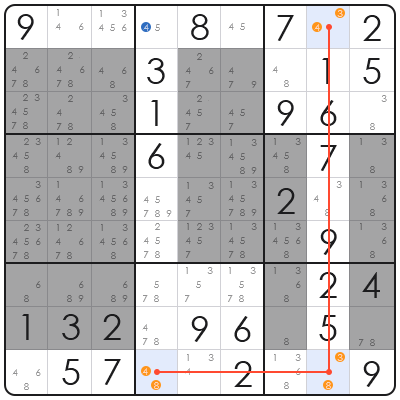
单元格 R1C4 就是一个“受害者”，因为它与钳子 1 在同一行，与钳子 2 在同一列。它的候选数是 {4, 5}。

逻辑推导：
让我们看看枢纽 (R9C8) 会发生什么。它只能是 3 或 8。

• 情况 1： 如果枢纽 R9C8 是 3，那么钳子 1 (R1C8) 就不能是 3，所以它必须是 4。
• 情况 2： 如果枢纽 R9C8 是 8，那么钳子 2 (R9C4) 就不能是 8，所以它必须是 4。

在所有可能的结果中，两个钳子中必有一个是 4。这意味着任何同时看到这两个钳子的单元格都绝不可能是 4。

由于 R1C4 同时看到了两个钳子，所以它不能是 4。我们可以放心地从它的候选数 {4, 5} 中排除 '4'，留下 {5} 作为解！

掌握这项高级技巧

这就是“Y-Wing”法的工作原理。这是一项进阶的数独策略，您可能需要花一些时间和练习才能熟练地识别它。