数独“X-Wing”法 (二链列) 解题技巧

什么是“X-Wing”法？

“X-Wing”（中文常称为“二链列”）是一种高级数独技巧，它基于两条平行的行或两条平行的列。使用此策略时，您不需要关注 3x3 的宫（Block），因为它们不参与此逻辑（只关注行和列）。

通过查看示例，我们将更容易理解这种技巧。

如何发现 X-Wing

当一个候选数（例如 '4'）满足以下条件时，就会形成 X-Wing 模式：

1. 在某一行中恰好出现在两个单元格中。
2. 在另一行中也恰好出现在两个单元格中。
3. 并且这四个单元格形成一个完美的矩形。

第一步：在两行中寻找模式

让我们看看两条平行的行：第 5 行 和 第 7 行。

在 第 5 行 中，候选数 '4' 仅出现在两个单元格中：

• R5C5 (笔记 {3, 4})
• R5C8 (笔记 {3, 4})

在 第 7 行 中，候选数 '4' 也仅出现在两个单元格中：

• R7C5 (笔记 {4, 6, 9})
• R7C8 (笔记 {4, 9})

这四个单元格 (R5C5, R5C8, R7C5, R7C8) 构成了一个矩形的四个角。

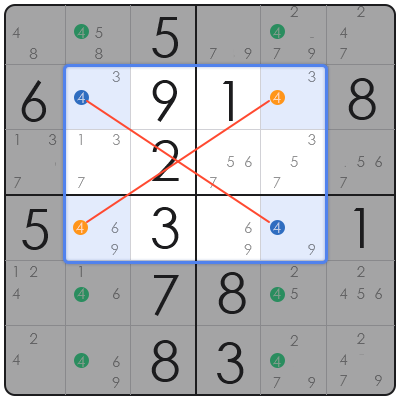
第二步：对角线逻辑

由于数字 4 不能在同一行或同一列中重复，我们可以放心地假设这两行中 '4' 的解必然是对角线关系的。

• 情况 1： 4 位于 R5C5 和 R7C8。
• 情况 2： 4 位于 R5C8 和 R7C5。

无论哪种情况，第 5 列中必然有一个 '4'，且第 8 列中也必然有一个 '4'。

第三步：从列中排除候选数

现在让我们把视角拉远，看看涉及的列。既然 第 5 列 和 第 8 列 中（在我们矩形的单元格里）必然存在 '4'，���么这两列中的其他任何单元格都不能是 4。

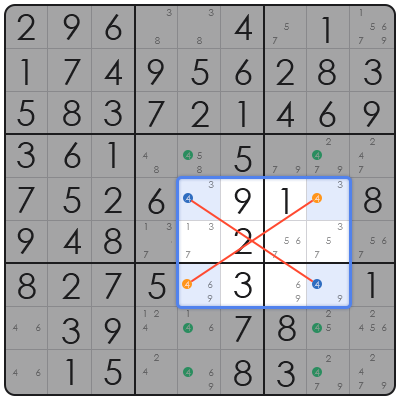
因此，我们可以自信地从这两列的剩余笔记中删除 '4'。

• 在第 5 列中： 我们从 R4C5, R8C5, 和 R9C5 的笔记中排除 '4'。
• 在第 8 列中： 我们从 R4C8, R8C8, 和 R9C8 的笔记中排除 '4'。

掌握这项高级技巧

现在您已经知道如何在数独中应用 X-Wing 技巧了！这是一种清理多余笔记的强力方法，也是学习下一个高级策略“Y-Wing”的基础。