数独“指向三链”法 (Pointing Triples) 解题技巧

什么是“指向三链” (Pointing Triple)？

“指向三链”技巧与“指向对 (Pointing Pairs)”非常相似，其工作原理也完全相同。 当某个候选数 (Note) 在一个 3x3 的宫（Block）内仅出现在三个单元格中，且这三个单元格恰好都属于同一行或同一列时，该技巧便适用。这意味着该数字必然是这三个单元格之一的解。

背后的逻辑

因为我们知道该数字必须位于这三个单元格之一，所以它显然不可能是同一行或同一列中（该宫之外）任何其他单元格的解。因此，我们可以从那些位置中将其排除。

如何发现指向三链

让我们看一个例子（例如在左上角的 3x3 宫）。

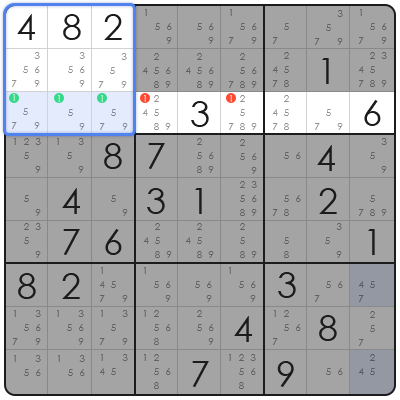
第一步：扫描宫内的候选数

我们扫描左上角宫内的所有候选数（笔记）。我们的目标是找到一个仅出现在同一条直线上的单元格里的数字。
在这个例子中，我们寻找候选数 '1'。我们发现所有可能包含数字 1 的单元格都位于同一行（例如：第 3 行）。

第二步：识别“指向三链”

数字 '1' 在这个宫内仅作为候选数出现在 R3C1, R3C2, 和 R3C3（举例）这三个单元格中。
这就形成了一个**“指向三链”**。逻辑是：数字 '1' 必须出现在这个宫的某个位置。既然这三个地方是它仅有的容身之处，那么其中之一必然是 1。

第三步：排除宫外的候选数

既然我们将这个宫的 '1' 锁定在了第 3 行，我们可以放心地从该行（在其他宫）的所有其他单元格中排除所有可能的 '1'。

得出这个结论后，为了避免混淆，可以安全地从第 3 行的其他笔记（即该行剩余的单元格）中删除所有可能的 '1'。

掌握这项技巧

请记住，您可以在宫、行和列中运用同样的把戏。这就是“指向三链”法的工作原理。一旦学会了它，您就可以开始练习了。