数独“显性数对” (Obvious Pairs) 解题技巧

什么是“显性数对” (Obvious Pairs)？

“显性数对”（通常也称为“显性数对”或 Naked Pairs）是一种基于候选数（笔记）的强大进阶技巧。
当同一个区域（3x3 宫、行或列）内的两个单元格仅包含完全相同的两个候选数时，就会出现这种模式。

背后的逻辑

逻辑很简单：如果单元格 A 和单元格 B 都只能是 '7' 或 '9'，那么数字 '7' 和 '9' 就被锁定在这两个单元格中。
因此，'7' 和 '9' 不可能存在于该区域（宫、行或列）的任何其他单元格中。我们的任务就是利用这个“锁定”关系来排除其他单元格中的候选数。

如何使用“显性数对”技巧

让我们看一个完美的例子，位于中下的 3x3 宫。

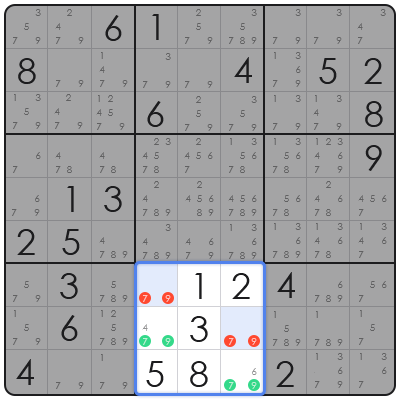
在这个宫里，我们可以看到以下已填入的数字和笔记：

• 已填数字： 1 (R7C5), 2 (R7C6), 3 (R8C5), 5 (R9C4), 8 (R9C5)。
• 笔记 (候选数)：R7C4 = {7, 9}R8C4 = {4, 7, 9}R8C6 = {7, 9}R9C6 = {6, 7, 9}

第一步：找到数对

仔细观察笔记。我们可以识别出：

• 单元格 R7C4 仅包含 {7, 9}。
• 单元格 R8C6 也仅包含 {7, 9}。 这两个单元格位于同一个宫内，构成了一个完美的**“显性数对”**。

第二步：排除候选数

根据我们的逻辑，既然 7 和 9 被锁定在 R7C4 和 R8C6 中，它们就不能出现在这个宫的任何其他单元格中。

• 我们现在必须从该宫的所有其他单元格中移除 '7' 和 '9' 的笔记。
• 对于 R8C4：其笔记是 {4, 7, 9}。移除 7 和 9 后，只剩下 {4}。
• 对于 R9C6：其笔记是 {6, 7, 9}。移除 7 和 9 后，只剩下 {6}。

第三步：找到新解

通过执行此排除操作，我们瞬间揭示了两个新的**“显性唯一数” (Obvious Singles)！

• 单元格 R8C4 现在必须是 4。
• 单元格 R9C6 现在必须是 6。

掌握这项进阶技巧

这就是“显性数对”技巧的威力。当谜题似乎陷入僵局时，它能帮助玩家找到突破口。一旦掌握，它将使解决困难（Hard）和专家（Expert）级数独谜题的速度大大加快！