數獨「顯性數對」 (Obvious Pairs) 解題技巧

什麼是「顯性數對」 (Obvious Pairs)？

「顯性數對」（通常也稱為「顯性數對」或 Naked Pairs）是一種基於候選數（筆記）的強大進階技巧。
當同一個區域（3x3 宮、行或列）內的兩個儲存格僅包含完全相同的兩個候選數時，就會出現這種模式。

背後的邏輯

邏輯很簡單：如果儲存格 A 和儲存格 B 都只能是 '7' 或 '9'，那麼數字 '7' 和 '9' 就被鎖定在這兩個儲存格中。
因此，'7' 和 '9' 不可能存在於該區域（宮、行或列）的任何其他儲存格中。我們的任務就是利用這個「鎖定」關係來排除其他儲存格中的候選數。

如何使用「顯性數對」技巧

讓我們看一個完美的例子，位於中下 的 3x3 宮。

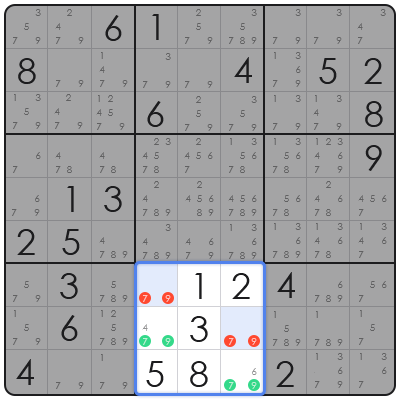
在這個宮裡，我們可以看到以下已填入的數字和筆記：

• 已填數字： 1 (R7C5), 2 (R7C6), 3 (R8C5), 5 (R9C4), 8 (R9C5)。
• 筆記 (候選數)：R7C4 = {7, 9}R8C4 = {4, 7, 9}R8C6 = {7, 9}R9C6 = {6, 7, 9}

第一步：找到數對

仔細觀察筆記。我們可以識別出：

• 儲存格 R7C4 僅包含 {7, 9}。
• 儲存格 R8C6 也僅包含 {7, 9}。 這兩個儲存格位於同一個宮內，構成了一個完美的**「顯性數對」。

第二步：排除候選數

根據我們的邏輯，既然 7 和 9 被鎖定在 R7C4 和 R8C6 中，它們就不能出現在這個宮的任何其他儲存格中。

• 我們現在必須從該宮的所有其他儲存格中移除 '7' 和 '9' 的筆記。
• 對於 R8C4：其筆記是 {4, 7, 9}。移除 7 和 9 後，只剩下 {4}。
• 對於 R9C6：其筆記是 {6, 7, 9}。移除 7 和 9 後，只剩下 {6}。

第三步：找到新解

透過執行此排除操作，我們瞬間揭示了兩個新的**「顯性唯一數」 (Obvious Singles)！

• 儲存格 R8C4 現在必須是 4。
• 儲存格 R9C6 現在必須是 6。

掌握這項進階技巧

這就是「顯性數對」技巧的威力。當謎題似乎陷入僵局時，它能幫助玩家找到突破口。一旦掌握，它將使解決困難（Hard）和專家（Expert）級數獨謎題的速度大大加快！