스도쿠 "포인팅 트리플" (Pointing Triples) 해결 기법

"포인팅 트리플"이란 무엇인가요?

"포인팅 트리플(Pointing Triples)" 기법은 "포인팅 페어(Pointing Pairs)"와 매우 유사하며 동일한 개념으로 작동합니다.
이는 특정 **후보수(Note)**가 3x3 블록 내의 오직 세 칸에만 존재하고, 그 세 칸이 모두 동일한 행이나 열에 속할 때 적용됩니다. 이는 해당 후보수가 반드시 이 세 칸 중 하나에 들어가야 함을 의미합니다.

그 배후의 논리

우리는 그 숫자가 이 세 칸 중 하나에 반드시 있어야 한다는 것을 알기 때문에, 동일한 행이나 열(블록 외부)에 있는 다른 어떤 칸의 정답도 될 수 없음이 분명합니다. 따라서 그 위치에서 해당 후보수를 제거할 수 있습니다.

포인팅 트리플을 찾는 방법

왼쪽 상단 (top-left) 3x3 블록의 예제를 살펴보겠습니다.

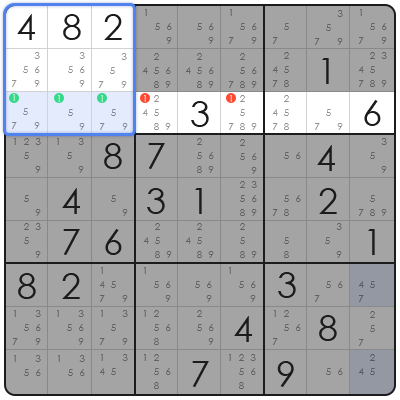
1단계: 블록 내부의 후보수 스캔

우리는 왼쪽 상단 블록 내부의 모든 후보수(메모)를 스캔합니다. 우리의 목표는 모두 같은 줄(line)에 있는 칸에만 나타나는 숫자를 찾는 것입니다.
이 예제에서는 후보수 **'1'**을 찾습니다. 숫자 1을 포함할 수 있는 모든 칸이 하나의 행(예: 행 3)에 위치해 있음을 발견했습니다.

2단계: "포인팅 트리플" 식별하기

숫자 **'1'**은 이 블록 내에서 오직 R3C1, R3C2, R3C3 (예시) 칸에서만 후보수로 나타납니다.
이것이 **"포인팅 트리플"**을 형성합니다. 논리는 다음과 같습니다: 숫자 '1'은 이 블록 내 어딘가에 반드시 나타나야 합니다. 있을 수 있는 곳이 이 세 곳뿐이므로, 그중 하나가 반드시 1이어야 합니다.

3단계: 블록 외부의 후보수 제거

이 블록에서 '1'을 행 3에 "고정(locked)"시켰으므로, 우리는 이 행(다른 블록)의 다른 모든 칸에서 다른 모든 가능한 '1'을 안전하게 제거할 수 있습니다.

이 결론을 내린 후, 혼동을 피하기 위해 행 3의 메모(행의 나머지 칸)에서 다른 모든 가능한 '1'을 안전하게 삭제할 수 있습니다.

이 기술을 마스터하세요

블록, 행, 열에 대해서도 같은 요령을 사용할 수 있다는 점을 기억하세요. 이것이 "포인팅 트리플" 기법이 작동하는 방식입니다. 일단 배우고 나면 연습을 시작할 수 있습니다.