스도쿠 "네이키드 페어" (Obvious Pairs) 해결 기법

"네이키드 페어" (Obvious Pair)란 무엇인가요?

"네이키드 페어" (Obvious Pair, 흔히 Naked Pair라고도 함)는 메모(후보수) 사용을 기반으로 하는 강력한 고급 기술입니다.
이 패턴은 동일한 하우스(3x3 블록, 행 또는 열) 내의 두 칸이 오직 그리고 정확히 동일한 두 개의 후보수만 포함할 때 발생합니다.

그 배후의 논리

논리는 다음과 같습니다. 만약 칸 A와 칸 B가 오직 '7' 또는 '9'만 될 수 있다면, 숫자 '7'과 '9'는 이 두 칸에 **고정(locked)**됩니다.
따라서 '7'과 '9'는 동일한 하우스(블록, 행 또는 열) 내의 다른 어떤 칸에도 존재할 수 없습니다. 우리의 임무는 이 "잠금"을 사용하여 다른 칸에서 후보수를 제거하는 것입니다.

"네이키드 페어" 기법 사용 방법

중앙 하단 3x3 블록의 완벽한 예제를 살펴보겠습니다.

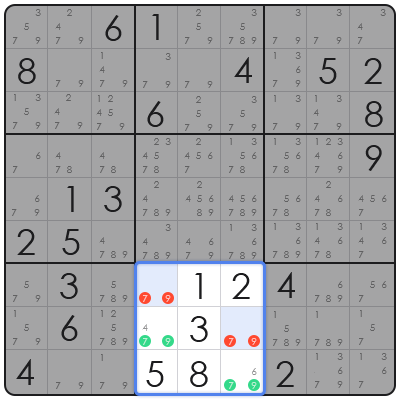
이 블록에서 다음과 같이 채워진 숫자와 메모를 볼 수 있습니다:

• 채워진 숫자: 1 (R7C5), 2 (R7C6), 3 (R8C5), 5 (R9C4), 8 (R9C5).
• 메모 (후보수):R7C4 = {7, 9}R8C4 = {4, 7, 9}R8C6 = {7, 9}R9C6 = {6, 7, 9}

1단계: 페어(Pair) 찾기

메모를 자세히 보세요. 우리는 다음을 식별할 수 있습니다:

• 칸 R7C4는 오직 **{7, 9}**만 포함합니다.
• 칸 R8C6도 오직 **{7, 9}**만 포함합니다. 이 두 칸은 같은 블록에 있으므로 완벽한 **"네이키드 페어"를 형성합니다.

2단계: 후보수 제거하기

우리의 논리에 따르면, 7과 9는 R7C4와 R8C6에 고정되어 있으므로 이 블록의 다른 어떤 칸에도 나타날 수 없습니다.

• 이제 우리는 이 블록의 다른 모든 칸에서 메모 '7'과 '9'를 제거해야 합니다.
• R8C4의 경우: 메모는 {4, 7, 9}입니다. 7과 9를 제거하면 {4}만 남습니다.
• R9C6의 경우: 메모는 {6, 7, 9}입니다. 7과 9를 제거하면 {6}만 남습니다.

3단계: 새로운 정답 찾기

이 제거 작업을 수행함으로써, 우리는 즉시 두 개의 새로운"네이키드 싱글(Obvious Singles)"을 발견했습니다!

• 칸 R8C4는 이제 반드시 4여야 합니다.
• 칸 R9C6은 이제 반드시 6이어야 합니다.

이 고급 기술을 마스터하세요

이것이 "네이키드 페어" 기법의 힘입니다. 퍼즐이 꽉 막힌 것처럼 보일 때 돌파구를 찾는 데 도움을 줍니다. 일단 마스터하면 '어려움(Hard)' 및 '전문가(Expert)' 레벨의 스도쿠 퍼즐을 훨씬 더 빨리 풀 수 있게 될 것입니다!