数独「ソードフィッシュ」解法テクニック (Swordfish)

「ソードフィッシュ」テクニックとは？

「ソードフィッシュ」 (Swordfish) は、数独の上級者向け攻略テクニックです。通常、「難しい (Hard)」や「エキスパート (Expert)」レベルの問題で、特定の候補数字を削除（除外）するために使用されます。

簡単に言えば、ソードフィッシュは「X-Wing（井桁の理）」と非常によく似ています。違いは、X-Wingが2つの行（または列）を使用するのに対し、ソードフィッシュは3つのセットを使用して論理的なループを形成する点です。

ソードフィッシュの見つけ方

理解を深めるために、実際の例を見てみましょう。

ステップ1：「フィッシュ数字」と基本セットを見つける

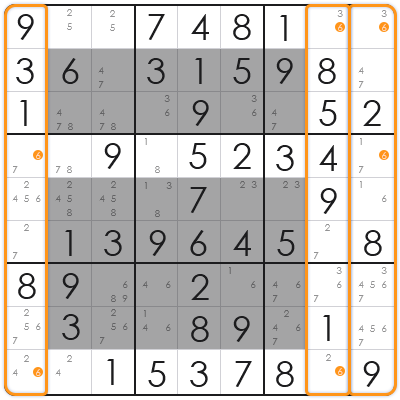
この問題では、数字の 6 が私たちの「フィッシュ数字」（ターゲット数字）です。候補数字の6が、**同じ3つの列（または行）にのみ現れるような3つの行（または列）**を探す必要があります。

例に示されているように、今回の基本セット (Base Sets) は 行1、行4、行9 です。
これら3つの行をスキャンすると、候補数字の6は 列1、列8、列9 にしか現れないことがわかります。

ステップ2：ロジック（2つの主な可能性）

数独のルールにより、候補数字の6は、これら3つの行（行1、行4、行9）のそれぞれに1回ずつ入らなければなりません。それらの位置が列1、8、9と完全に一致しているため、解法には2つの主要な「対角線」パターンしか存在しません。

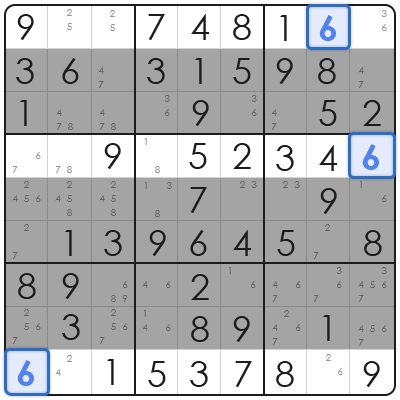
ケース1：
6が入るパターンは次のようになります：R1C8（行1列8）、R4C9（行4列9）、R9C1（行9列1）。

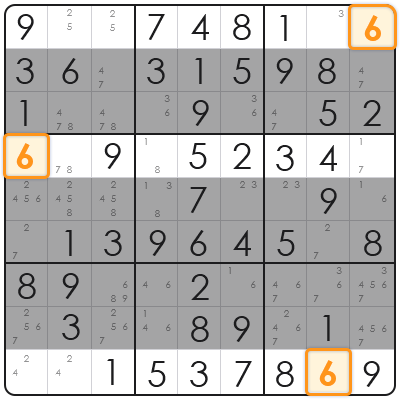
ケース2：
あるいは、次のパターンになります：R1C9（行1列9）、R4C1（行4列1）、R9C8（行9列8）。

ステップ3：候補数字を削除（除外）する

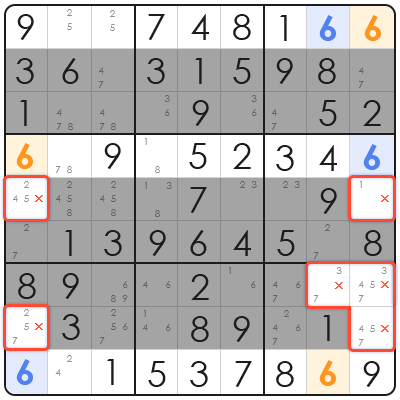
最終的にどちらのケースが正しいとしても、これら3つの基本セット（行1、4、9）は、整列した列（列1、8、9）の位置を必ずカバーします。つまり、これらの行の6は、必ずこれら3つの列の中に収まる必要があります。

結論： これら3つの列（列1、8、9）において、（ソードフィッシュの構成マス以外の）他のどのマスにも6を入れることはできません。

したがって、これら3つの列にある他のすべてのメモから6を安全に削除できます（つまり、行2、3、5、6、7、8 の対象列から6を除外します）。

この上級テクニックをマスターしよう

これで、数独で「ソードフィッシュ」テクニックを適用する方法がわかりました。盤面上で肉眼で見つけるのは難しいですが、一度マスターすれば、膠着状態（デッドロック）を打破するための非常に強力な武器になります。