数独「ポインティング・トリプル」(Pointing Triples) 解法テクニック

「ポインティング・トリプル」とは？

「ポインティング・トリプル」テクニックは、「ポインティング・ペア」と非常によく似ており、同じ概念に基づいています。 これは、特定のメモ（候補数字）が、3x3のブロック内の3つのマスにのみ存在し、かつその3つのマスがすべて同じ行または列に属している場合に適用されます。これは、その候補数字がこれら3つのマスのうちの1つの正解でなければならないことを意味します。

その背後にあるロジック

その数字がこれら3つのマスのいずれかに必ず入ることがわかっているため、同じ行または列（ブロックの外側）にある他のどのマスにとっても、それは正解にはなり得ません。したがって、それらのマスから削除することができます。

ポインティング・トリプルの見つけ方

左上（top-left）の3x3ブロックにある例を見てみましょう。

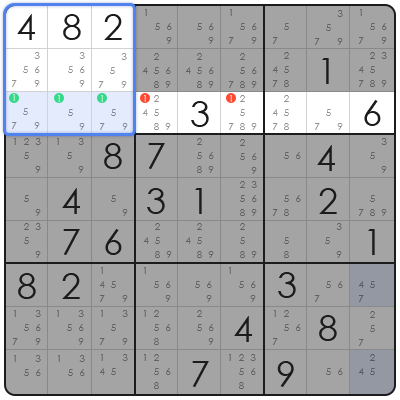
ステップ1：ブロック内のメモをスキャンする

左上のブロック内にあるすべてのメモをスキャンします。私たちの目標は、すべて同じ直線上にあるマスにのみ現れる数字を見つけることです。
この例では、候補数字 '1' を探します。数字の1が含まれる可能性のあるすべてのマスが、1つの行（例：行3）に位置していることがわかります。

ステップ2：「ポインティング・トリプル」を特定する

数字の '1' は、このブロック内では R3C1、R3C2、R3C3（例として）のマスにのみ候補として現れます。
これが**「ポインティング・トリプル」**を形成します。ロジックはこうです：数字の '1' はこのブロック内のどこかに必ず現れなければなりません。これら3か所しかあり得ないため、そのうちのどれかが必ず1になります。

ステップ3：ブロックの外にあるメモを削除する

このブロックの '1' を行3に「ロック（固定）」したため、この行（他のブロック）の他のすべてのマスから、他のすべての可能な '1' を安全に削除できます。

この結論の後、混乱を避けるために、行3のメモ（行の残りのマス）から他のすべての可能な '1' を安全に削除できます。

このテクニックをマスターしよう

ブロック、行、列に対しても同じトリックを使用できることを覚えておいてください。これが「ポインティング・トリプル」テクニックの仕組みです。一度学べば、練習を始めることができます。