"Pointing Triples" Technique

What is a "Pointing Triple"?

The "Pointing Triples" technique is very similar to "Pointing Pairs" and works on the same concept.

It applies if a specific Note (candidate) is present in only three cells of a 3x3 block, and all three of those cells also belong to the same row or column. This means that the Note must be a solution for one of these three cells.

The Logic Behind It

Because we know that number must be in one of those three cells, it obviously can't be a solution for any other cell in that same row or column (outside the block). Therefore, it can be eliminated from them.

How to Find a Pointing Triple

Let's take a look at an example in the top-left 3x3 block.

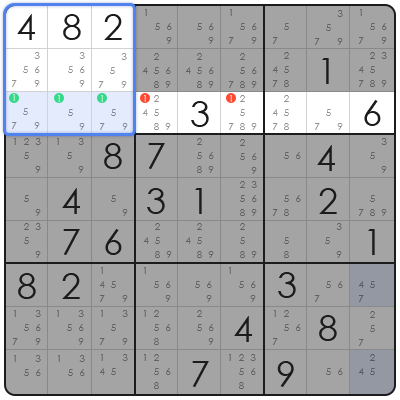
Step 1: Scan the Notes Inside the Block

We scan all the notes inside the top-left block. Our goal is to find a number that only appears in cells that are all on the same line

In this example, we look for the candidate '1'. We find that all the cells that might contain the number 1 are located in one row (e.g., Row 3).

Step 2: Identify the "Pointing Triple"

The number '1' appears as a candidate in this block only in cells R3C1, R3C2, and R3C3 (as an example).

This forms a "Pointing Triple." The logic is: The number '1' must appear somewhere in this block. Since these are the only three places it can be, one of them must be the 1.

Step 3: Eliminate Notes Outside the Block

Since we have locked the '1' for this block into Row 3, we can safely eliminate all other possible '1's from all other cells of this row (in other blocks).

After this conclusion, all other possible '1's can be safely deleted from the Notes of Row 3 (in cells R3C1 through R3C6) to avoid confusion.

Master This Technique

Remember that you can do the same trick for blocks, rows, and columns. That is how the "Pointing Triples" technique works. Once you have learned it, you can get some practice.